Basics of Deep Learning p.14 - How to train a Neural Net

---

​This post is part of a series:

• Part 1: Introduction
• Part 2: Feedforward Algorithm explained
• Part 3: Implementing the Feedforward Algorithm in pure Python
• Part 4: Implementing the Feedforward Algorithm in pure Python cont'd
• Part 5: Implementing the Feedforward Algorithm with NumPy
• Part 6: Backpropagation explained - Cost Function and Derivatives
• Part 7: Backpropagation explained - Gradient Descent and Partial Derivatives
• Part 8: Backpropagation explained - Chain Rule and Activation Function
• Part 9: Backpropagation explained Step by Step
• Part 10: Backpropagation explained Step by Step cont'd
• Part 11: Backpropagation explained Step by Step cont'd
• Part 12: Backpropagation explained Step by Step cont'd
• Part 13: Implementing the Backpropagation Algorithm with NumPy
• Part 14: How to train a Neural Net​

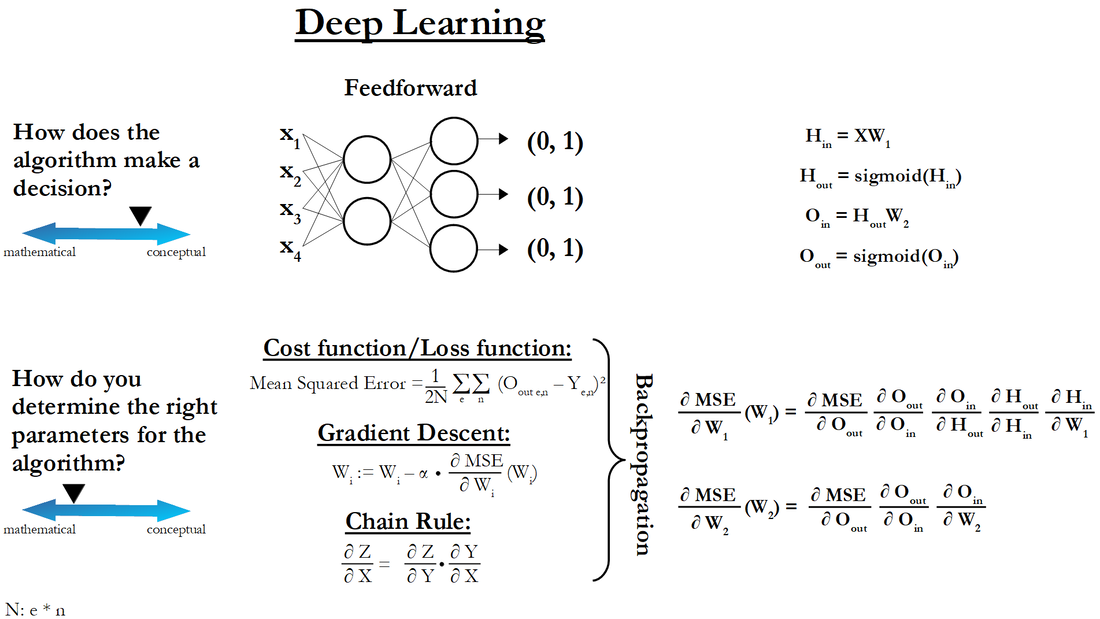
Here are the corresponding Jupyter Notebooks for this post:

• Notebook 1
• Notebook 2

---

In the previous post, we’ve implemented the backpropagation algorithm in code and with that we then executed one gradient descent step. Thereby, we could reduce the MSE somewhat, but the improvement was only very small.

So, we have to do many more gradient descent steps. The question then was: When should we stop training the neural net? Or in other words, what does the training process of a neural net generally look like? And that’s what we are going to cover in this post.
​

​Monitoring MSE

So, our original goal for the neural net was to find such weights that the MSE would be minimized. Therefore, an easy approach to make sure that the neural net is able to make correct predictions, is to simply monitor how the MSE changes over the course of doing many gradient descent steps. This way, we can see how it behaves and then accordingly adjust our learning rate or our neural net if necessary.
​
So, that’s what we are going to do. But before we get into the code, let’s think about how the MSE ideally should behave as we execute our gradient descent steps.

Therefore, we are going to look again at a simpler function than our MSE, namely “x²”.

               See code cell 2 in Jupyter Notebook 1

So, let’s see what the ideal training scenario for this function looks like.

               See code cell 5 in Jupyter Notebook 1

In the left plot, we can see the gradient descent steps that we took on the actual function. And, as you can see, it looks like that we reach the minimum. But the value of x after the last step is 0.03. So, we are only very close to the minimum (which is at “x=0”).

In the right plot, we can see how the value of the function changes with each gradient descent step. So, at the start (Gradient Descent Step 0), x is still 5. So, accordingly the value of the function is 25. And then, with each step it gets smaller and smaller until it is almost zero. And at that point, we can stop training the neural net.

So, this is how the function (in our case then the MSE) ideally should behave as we execute the gradient descent algorithm. In the beginning, it should drop off pretty quickly because we are taking large steps towards the minimum. And then, the decrease should taper off as we get closer and closer to the minimum and therefore take smaller and smaller steps.

So, this is what the ideal scenario of applying the gradient descent algorithm looks like. And this is then also what we are looking for when we train our neural net. But, before we get to that, let’s see how the “x²”-function behaves if the learning rate is either too small or too big.

So, let’s start with a learning rate that is too small.

               See code cell 6 in Jupyter Notebook 1

In this case, as you can see, the curve in the right plot is basically linear. This is a clear sign that the learning rate is too small. And in the left plot, you can also see that we barely moved away from our starting point. So, we are still very far away from the minimum.

We could, however, simply do more steps to get closer to it. So, let’s do that.

               See code cell 7 in Jupyter Notebook 1

Now, the curve in the right plot starts to bend a little bit. So, we seem to get closer to the shape that we saw before. But, as you can see in the left plot, we are still far away from the minimum. So, let’s do 1000 steps.

               See code cell 8 in Jupyter Notebook 1

Now, we have gotten very close to the minimum. And the curve in the right plot looks basically as before in the ideal scenario (code cell 5). In the beginning, it drops off pretty quick and then the decrease tapers off.

So, there is a trade-off between the learning rate and the number of gradient descent steps that we need to do. With this very small learning rate, we also get to the minimum but we need 1000 steps to do that. Whereas before, with the learning rate of 0.2 (code cell 5), we only needed 10 steps to achieve a similar result.

So, you might be tempted to set the learning rate even higher than 0.2 to get even faster to the minimum. But you also have to be careful with that.

So, let’s set it for example to 0.9.

               See code cell 9 in Jupyter Notebook 1

In this case, we are always overshooting the minimum with every step. But we, nonetheless, get closer and closer to it. The final step, however, is only at 0.54. Whereas, before at a learning rate of 0.2 (code cell 5), it was already at 0.03 after 10 steps. So again, we would have to make more steps to get closer to the minimum.

So, as you can see, a higher learning rate doesn’t guarantee that you will get faster to the minimum. In fact, it can even be the cause that you will never reach the minimum. For example, let’s set the learning rate to 1.1.

               See code cell 10 in Jupyter Notebook 1

In this case, we overshoot the minimum so much with every step that we end up at a higher point on the function. And this just keeps escalating. And that’s why the curve in the right plot actually increases instead of decreasing. This is a clear sign that the learning rate is way too high.

So, to recap, for training a neural net, there is a balancing act between the learning rate and the number of gradient descent steps that you want to take. On the one hand, you want the learning rate to be as large as possible so that the run time of the gradient descent algorithm is as fast as possible. But, on the other hand, the learning rate should be as low as necessary to make sure that the cost function actually decreases.

And as another general rule of thumb for the training process, let’s say you have a curve in the right plot that has the ideal shape (code cell 5) but instead of going down to almost zero, it already tapers off at for example 5 or maybe at 10. In that case, the neural net is probably too small to capture the patterns in the data. So, to get around that, what you can do is to increase the size of the neural net by either adding more layers or by adding more nodes within the layers.

​Code

So, this is what the training process generally looks like. So, let’s now apply it to our neural net.
​
               See Jupyter Notebook 2

Therefor, we simply put the feedforward and the backpropagation algorithms into a for-loop.

               See code cell 5 in Jupyter Notebook 2

In the context of deep learning, each iteration of such a for-loop, by the way, is called an “epoch”. Additionally, we also calculate the MSE and accuracy after every feedforward algorithm and store those values into a dictionary. That way we can see, how they change after each epoch.

​Training the Neural Net

Looking at the plots after our first training attempt, we can see that the plot on the left side doesn’t really have the ideal shape that we want to see (code cell 5 in Jupyter Notebook 1).
​
               See code cell 6 in Jupyter Notebook 2

It is still pointing downward, and it is not flattened out yet. Additionally, the behavior of the accuracy in the right plot looks weird. It bounces between 35% and 65%. So, let’s train the neural net for a longer time. So, let’s do 10,000 epochs instead of just 1,000.

               See code cells 7-8 in Jupyter Notebook 2

And now, the curve in the left plot looks more like the ideal curve (code cell 5 in Jupyter Notebook 1). We got down to below an MSE of 0.06 and the accuracy is very close to one. But let’s train the neural net for an even longer time, namely 15,000 epochs, to see if the MSE and accuracy get even better.

               See code cells 9-10 in Jupyter Notebook 2

Here, the MSE decreased a little bit more and the accuracy increased also a little bit more. But, I think, now we can stop training because there is not much more improvement to be expected.

So, let’s now see how good the neural net is at predicting flowers that it hasn’t seen before. So, the flowers from our test set.

               See code cells 11-12 in Jupyter Notebook 2

And, as you can see, the accuracy is 95%. So, I think, it should be clear that the neural net has learned how to distinguish the different flowers.

​Different Train-Test-Split and Starting Values for the Weights

And now, before I wrap up this post, let’s see what happens if we have different flowers in our training and testing data set. So, we are going set the random state in the train test split function to 7 (before it was 4).
​
               See code cell 13 in Jupyter Notebook 2

And let’s also use different weights. So, we are going to set the random seed to 3 (before it was 10).

               See code cell 14 in Jupyter Notebook 2

So, if we now train the neural net with these specific training flowers and starting weights and look at the graphs, then we have a problem.

               See code cell 15 in Jupyter Notebook 2

The MSE looks similar to our ideal curve (code cell 5 in Jupyter Notebook 1), but it already tapers off at about 0.111. On top of that, the accuracy is just at 0.35. So, it basically guesses randomly.

So, for some reason, either because of the different train test split or because we chose a different starting point for the gradient descent algorithm, the neural net wasn’t able to learn the patterns in the data.

To solve this problem, we have to use the second rule of thumb that I mentioned earlier in this post and make the neural net bigger. And since adding another hidden layer to the net would require us to alter too much of our code, let’s just increase the number of nodes in the hidden layer. And we are going to set it to 6 (before we had 2 nodes).

               See code cell 16 in Jupyter Notebook 2

So, let’s train the neural net again and look at the plots.

               See code cell 17 in Jupyter Notebook 2

So now, the MSE goes even below 0.02 and the accuracy gets close to one again. So, let’s see how good the neural net is at predicting the test flowers.

               See code cells 18-19 in Jupyter Notebook 2

And we get an accuracy of 90%. So, also in this case the neural net learned how to distinguish the different flowers.

So now, we have finally answered the two questions that we stated in the first post of this series.

And with that, we have reached the end of this series.
​
PS: If you want to see how to code a neural net from start to finish (for another data set), you can check out this post.